Entradas

Matriz de transición

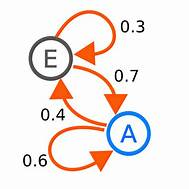
Imagen
Matriz de transición. Evento estocástico. Un evento estocástico es aquel que no se puede predecir de manera determinista. Un proceso estocástico es un conjunto de variables aleatorias que dependen de un parámetro o argumento. En el análisis de series temporales, este parámetro suele ser el tiempo. Formalmente, se define como una familia de variables aleatorias e indexadas por el tiempo t , de modo que para cada valor de t , y tiene una distribución de probabilidad específica. Cadena de Marlov. En la teoría de la probabilidad, una cadena de Márkov (también conocida como modelo de Márkov) es un tipo especial de proceso estocástico discreto. En este proceso, la probabilidad de que ocurra un evento depende solamente del evento inmediatamente anterior. Esta característica de incluir una memoria reciente se llama propiedad de Markov. A diferencia de eventos independientes que no tienen memoria de ningún evento anterior, en una cadena de Márkov, cada evento está conectado al evento anterior.
Publicar un comentario
Leer más

Inversa de una matriz

Imagen
Inversa de una matriz. En matemáticas, una matriz inversa es una matriz cuadrada que, al multiplicarse por la matriz original, produce la matriz identidad. La matriz identidad es una matriz cuadrada en la que todos los elementos de la diagonal principal son 1 y el resto son 0. En otras palabras, si A es una matriz cuadrada invertible, entonces su matriz inversa se denota por A -1 y cumple la siguiente propiedad: A -1   A = I = A  A -1 Donde I es la matriz identidad. No todas las matrices son invertibles. Ejemplo: Determine la matriz inversa, si tiene, de la matriz A. Si la matriz A tiene inversa, entonces: Es decir: (1)   3a + 5c = 1 (2)   a + 6c = 0   (3)   3b + 5d = 0 (4)   b + 6d = 1 Despejando a de (2) a = -6c Reemplazando en (1) 3(-6c) + 5c = 1 -18c + 5c = 1 -13c = 1 c = -1/13 Reemplazando en el despeje de a a = -6c a =-6(-1/13) a = 6/13 Despejando b de (4) b = 1 - 6d Reemplazando en (3) 3(1-6d) + 5d = 0 3 -18d + 5d = 0 -13d = -3 d = 3/13 Reemplazando en el despeje de b b = 1 -6(
Publicar un comentario
Leer más

Multiplicación de matrices

Imagen
 Multiplicación de matrices La multiplicación de matrices es una operación fundamental en matemáticas y se utiliza para combinar dos matrices en una nueva matriz. Verifica la compatibilidad: Asegúrate de que el número de columnas de la primera matriz sea igual al número de filas de la segunda matriz. Solo se pueden multiplicar matrices si cumplen con esta condición. Para calcular la multiplicación de dos matrices, debemos multiplicar las filas de la matriz de la izquierda por las columnas de la matriz de la derecha. Finalmente sumar el resultado de cada elemento. Sea A una matriz de m por n y B una matriz n por p y C  la matriz resultante de la multiplicación de la matriz de A por B, es decir: C = AB La matriz resultante será de tamaño m por p. El primer elemento de C para la primera se obtiene de multiplicar cada elemento de la fila 1 de A por cada elemento de la columna 1 de la matriz B y luego sumar esos productos, es decir: c 11 = a 11  b 11  + a 12  b 21  + ... + a 1n  b n1  El s
Publicar un comentario
Leer más

Matrices suma y resta de ...

Imagen
 Matrices Una matriz es una disposición rectangular de números, variables o expresiones matemáticas. Se representa entre paréntesis y sus elementos se disponen por filas y columnas. El tamaño de una matriz representa la cantidad de filas y columnas, así una matriz de 3 x 2, es una matriz de 3 filas y dos columnas. Ejemplo: En la imagen se ve la matriz A de tamaño de 3 x 3 y la matriz B tiene un tamaño de 2 x 3. Cada elemento de la matriz a ij y b ij  se puede hacer referencia según su posición donde i representa la fila y j a la columna. Las matrices se pueden clasificar según su tamaño, número de filas y columnas, o tipo de elementos. Algunos tipos comunes de matrices son: Matriz cuadrada : tiene el mismo número de filas y columnas. Como la matriz A. Matriz rectangular : tiene un número diferente de filas y columnas. Como la matriz B. Matriz diagonal : tiene elementos no nulos solo en la diagonal principal. Matriz triangular : tiene elementos nulos por encima o por debajo de la diago
Publicar un comentario
Leer más

Desigualdades cuadráticas

Imagen
 Desigualdades cuadráticas Las desigualdades cuadráticas tienen la forma:                  ax 2 + bx + c < 0  o bien:  ax 2  + bx + c ≤ 0  o bien:  ax 2  + bx + c > 0  o bien:  ax 2  + bx + c ≥ 0  La forma de solucionarlo es: Buscar los 2 posibles valores que dieran solución como si se tratase de una ecuación. Dibujar esos valores en una línea recta y  Probar la desigualdad con valores de los 3 rangos en los que se secciona la recta. Ejemplo: Resuelva la desigualdad:      2x 2 - x  > 6 2x 2  - x  - 6 > 0 (2x + 3) (x -2) > 0 Si fuese una ecuación  (2x + 3) (x -2) = 0  cada factor se iguala a cero, así que un valor sería: 2x + 3 = 0, es decir, x = -3/2 Y el otro: x - 2 = 0, es decir, x = 2 En una línea recta tendríamos: Los puntos en la línea nos muestra los siguientes rangos:  x < -3/2  -3/2 < x < 2  x > 2 Si evaluamos el rango x < -3/2 con x = -2 tenemos:    2(-2) 2  - (-2)  > 6 8 + 2 > 6 Este rango cumple con la desigualdad Probemos con x = 1,
Publicar un comentario
Leer más

Desigualdades lineales

Imagen
Desigualdades Una desigualdad es una expresión matemática que indica que dos valores no son iguales. En otras palabras, una desigualdad nos dice que hay una diferencia entre dos cantidades. Tipos de desigualdades: Desigualdad estricta: Esta es la forma más común de desigualdad. Se indica con el símbolo ≠. Por ejemplo, 5 ≠ 3 significa que 5 no es igual a 3. Desigualdad no estricta: Este tipo de desigualdad indica que dos valores pueden ser iguales o diferentes. Se indica con los símbolos ≤ o ≥. Por ejemplo, 2 ≤ 5 significa que 2 es menor o igual que 5, y 5 ≥ 2 significa que 5 es mayor o igual que 2. Ejemplos de desigualdades: 7 > 4 (7 es mayor que 4) 3 < 6 (3 es menor que 6) 5 ≠ 5 (5 no es igual a 5) 10 ≤ 10 (10 es menor o igual que 10) 12 ≥ 8 (12 es mayor o igual que 8) Las desigualdades se utilizan en muchas áreas de las matemáticas y la ciencia, incluyendo: Álgebra: Para resolver ecuaciones y desigualdades. Geometría: Para comparar longitudes, áreas y volúmenes. Física: Para de
Publicar un comentario
Leer más

Conjuntos

Imagen
Conjuntos Un conjunto es una colección de objetos que comparten una o más características en común. Los objetos que forman parte de un conjunto se llaman elementos. Tipos de conjuntos: Conjunto finito : Un conjunto con un número finito de elementos. Por ejemplo, el conjunto de los números pares del 1 al 10. Conjunto infinito : Un conjunto con un número infinito de elementos. Por ejemplo, el conjunto de todos los números naturales. Conjunto de números reales entre 1 y 2. Conjunto vacío : Un conjunto que no tiene ningún elemento. Se representa por {}. Conjunto unitario : Un conjunto que tiene un solo elemento. Ejemplos de conjuntos: Conjunto de los colores primarios: {rojo, amarillo, azul} Conjunto de los planetas del sistema solar: {Mercurio, Venus, Tierra, Marte, Júpiter, Saturno, Urano, Neptuno} Conjunto de los números pares: {2, 4, 6, 8, 10, ...} Conjunto de los números impares: {1, 3, 5, 7, 9, ...} Los conjuntos se pueden representar de diferentes maneras: Por extensión : Listando t
Publicar un comentario
Leer más