Interés compuesto.

Una de las principales aplicaciones de las funciones exponenciales y logarítmicas es en el tema de inversiones o préstamos a interés compuesto.

Las inversiones a interés compuesto implica que cuando se invierte un capital C, después de un período este gana una cierta cantidad de intereses I, los cuales son reinvertidos para que en el siguiente período los intereses se calculen sobre un monto M que es igual al capital del período anterior más los intereses de dicho período (M = C + I).

Después de varios períodos el monto acumulado de esa inversión se puede calcular con:

M = C(1 + (i/p))^np

Donde:

M es el monto o valor futuro.
C es el capital o valor presente.
i es la tasa de interés nominal anual.
n es el número de años.
p es la frecuencia (número de veces) de conversión de los intereses en un año.

En el caso de los prestamos a interés compuesto cada pago se hace sobre saldos insolutos, es decir, los intereses solo se calcularán sobre la deuda vigente y no la deuda original.

Tasa efectiva.

La tasa efectiva, también conocida como tasa efectiva anual (TEA), tasa de interés anual efectiva o tasa anual equivalente, es un indicador financiero que hace referencia al interés real que se paga o se gana al final de un periodo de tiempo determinado, teniendo en cuenta la capitalización de los intereses.

En otras palabras, la tasa efectiva refleja el costo real de un préstamo o la rentabilidad real de una inversión, considerando que los intereses se reinvierten y generan nuevos intereses a lo largo del tiempo.

Diferencias entre tasa nominal y tasa efectiva:

1. La tasa nominal es el porcentaje de interés que se aplica al capital inicial sin considerar la capitalización.
2. La tasa efectiva es mayor que la tasa nominal cuando hay capitalización de intereses.

Cálculo de la tasa efectiva:

La tasa efectiva e se calcula utilizando la siguiente fórmula:

e = (1 + ⁱ/_p)^p - 1

Donde:

e: Tasa efectiva anual

i: Tasa de interés nominal

p: Número de periodos de capitalización en un año

Ejemplo:

Si un préstamo tiene una tasa de interés nominal del 10% anual y se capitaliza mensualmente (n = 12), la tasa efectiva sería:

e = (1 + ^0.1/₁₂)¹² - 1 = 10.47%

Composición continua.

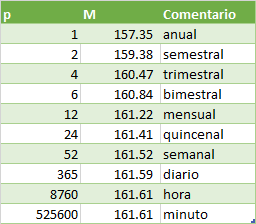
Suponga que invierte $100 en una cuenta que paga una tasa nominal anualizada del 12%, dependiendo de la frecuencia de conversión p tenemos los siguientes resultados dentro de 4 años. 

La tabla muestra estos valores para diferentes valores de p. Primero damos p = 1, 2 y 4 y después p = 12, 24, 52 y 365, que corresponden respectivamente a composición mensual, quincenal semanal y diaria. Los últimos, por comparación damos para p = 8760 y para p = 525600. Puede verse que conforme la frecuencia de composición se incrementa, el valor de la inversión también aumenta; sin embargo, no aumenta de manera indefinida, sino que se hace cada vez más cercana a cierto valor. Al centavo más significativo, no hay diferencia entre componerlo 8,760 veces en un año y componerlo 525,600 veces en un año; el valor de la inversión después de 4 años aún será $ 161.61.

La composición continua en el interés compuesto es un método para calcular el valor futuro de una inversión que asume que los intereses se ganan y reinvierten continuamente a lo largo del tiempo, en lugar de hacerlo en períodos discretos (como anualmente, semestralmente o mensualmente).

En la composición continua, el interés se calcula sobre el capital inicial más el interés que ya se ha ganado. Esto significa que el interés se gana sobre una base cada vez mayor, lo que lleva a un crecimiento exponencial del valor de la inversión a lo largo del tiempo.

Para calcular el valor futuro de una inversión con interés compuesto continuo, se utiliza la siguiente fórmula:

M = C * e^(n*i)

donde:

M es el valor de la inversión al final del período de tiempo.

C es el valor inicial de la inversión.

e es la constante matemática aproximadamente igual a 2.71828.

i es la tasa de interés anualizada.

n es el tiempo en años.

En el ejemplo anterior, donde invertíamos $100 a 12% en 4 años tendríamos:

M = C * e^(n*i) = 100 e^(4(0.12)) =  100 e^(0.48) = $161.61

Ejemplo:

Si inviertes $1000 a una tasa de interés anual del 5% con interés compuesto continuo, el valor futuro de la inversión después de 10 años sería:

Valor futuro = 1000 * e^(0.05*10) = 1648.72

En este caso, la inversión habría crecido a $1,648.72 después de 10 años, lo que representa un crecimiento del 64.87%.

Ventajas de la composición continua:

La composición continua genera un mayor crecimiento del valor de la inversión a lo largo del tiempo en comparación con la composición discreta.

Es un método más realista para calcular el valor futuro de una inversión, ya que asume que los intereses se ganan y reinvierten continuamente.

Desventajas de la composición continua:

Es un método más complejo de calcular que la composición discreta.

Requiere el uso de calculadoras especiales o software para obtener resultados precisos.

En resumen, la composición continua es un método para calcular el valor futuro de una inversión que asume que los intereses se ganan y reinvierten continuamente a lo largo del tiempo. Este método genera un mayor crecimiento del valor de la inversión a lo largo del tiempo en comparación con la composición discreta, pero es más complejo de calcular.