La línea recta y ecuaciones lineales.
Introducción.
Una relación entre dos variables por lo regular se expresa mediante de una ecuación algebraica que contiene las dos variables. Por ejemplo, si x es la longitud (en centímetros) del lado de un cuadrado y si y es su área (en centímetros cuadrados), entonces la relación entre x y y se expresa por la ecuación y = x2. Para cada valor de x, el valor respectivo de y se obtiene elevando al cuadrado el valor de x.
Las expresiones algebraicas se pueden representar en gráficas, en planos cartesianos.
Imagen 1: plano cartesiano
En un plano cartesiano, el eje horizontal generalmente se toma como el eje de las x (la variable independiente de las funciones o ecuaciones) y el eje vertical para la variable dependiente y.
En el punto donde los ejes se interceptan: x = 0 y y= 0.
La manera de demostrarlo es con el teorema de Pitágoras. Afirma que en todo triángulo rectángulo, la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
En la imagen d es la distancia entre A y B, el lado a uno de los catetos y el lado b el otro cateto, la longitud de a es igual a x2 - x1 y la de b es igual a y2 - y1, es decir:
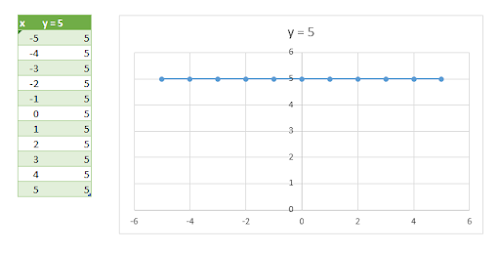
Una recta con pendiente cero sería de la forma y = b. Esta recta sería paralela al eje de la x, es decir, horizontal y para todo valor de x, y = b Por ejemplo la función f(x) = y = 5. Al graficar esta recta tendríamos:
Una recta con pendiente indefinida es aquella que es paralela al eje y. Para este tipo de recta, no importa el valor de la y, la x se mantiene constante. Una ecuación para este tipo de recta es x = a. Por ejemplo x = 5
Puntos en el plano.
Un punto en el plano cartesiano se representa con un par de números entre paréntesis; el primer valor representa a x y el segundo a y, por ejemplo:
- (-4, 3)
- (3, 2)
- (-4, -2)
- (4, -3)
Llamemos a cada punto A, B, C y D respectivamente. Para dibujarlos buscamos el valor en cada uno de los ejes y pintamos una línea punteada perpendicular a cada eje, en la intersección de dichas rectas se encontrará el punto. La siguiente imagen muestra los puntos.
Imagen 3: Cuadrantes del plano cartesiano.
- Primer cuadrante: x y y positivos (ambos mayores que cero)
- Segundo cuadrante: y positivo, x negativo
- Tercer cuadrante: x y y negativos (ambos menores a cero)
- Cuarto cuadrante: y negativo y x positivo
Distancia entre 2 puntos.
La distancia entre dos puntos (x1, y1) y (x2, y2) esta dado por la siguiente fórmula:
Es decir la longitud de la hipotenusa es la raíz cuadrada de la suma de sus catetos.
En la imagen se muestra dos puntos A(x1, y1) = (1, 3) y B(x2, y2) = (4, 8)
Imagen 4: distancia entre dos puntos.
En la imagen d es la distancia entre A y B, el lado a uno de los catetos y el lado b el otro cateto, la longitud de a es igual a x2 - x1 y la de b es igual a y2 - y1, es decir:
a = 4 - 1 = 3
b = 8 - 3 = 5
Luego entonces la longitud d; la distancia entre los dos puntos es:
d = √
(3)2 + (5)2
= √ (9) + (25) = 5.831
Línea recta.
Una línea recta es una figura geométrica que se extiende en una sola dirección sin curvaturas ni dobleces. Se caracteriza por:
- No tener principio ni fin: Se extiende infinitamente en ambos sentidos.
- Solo tiene una dimensión, la longitud.
- Contener un número infinito de puntos: Todos los puntos que se encuentran en la misma dirección que la línea recta forman parte de ella.
Representación:
En geometría, las líneas rectas se suelen representar con una letra minúscula, como r o s.
En un plano cartesiano, las líneas rectas se pueden representar mediante una ecuación.
Ecuación lineal
Una ecuación lineal es una ecuación de primer grado, es decir, que la variable con mayor exponente es 1. La forma general de una ecuación lineal es:
y = mx + b
donde:
- y es la variable dependiente.
- x es la variable independiente.
- m es la pendiente de la recta.
- b es el intercepto en el eje y. También conocida como ordenada al origen.
Interpretación:
La pendiente (m) indica la inclinación de la recta.
El intercepto en el eje y (b) indica el punto donde la recta cruza el eje y.
Ejemplos:
y = 2x + 3: Esta ecuación representa una recta con una pendiente de 2 y un intercepto en el eje y de 3.
y = -x + 1: Esta ecuación representa una recta con una pendiente de -1 y un intercepto en el eje y de 1.
Pendiente:
Si la pendiente m de una línea es positiva, la línea asciende hacia la derecha. Cuanto más grande sea el valor de m, la inclinación de la línea será mayor con respecto a la horizontal. Si m es negativa, la línea desciende hacia la derecha. Si m = 0, la línea es horizontal.
Imagen 5: Pendiente de una línea.
Para calcular la pendiente de una recta entre dos puntos (x1, y1) y (x2, y2) podemos ocupar la siguiente formula:
Imagen 6: recta con pendiente cero.
Una recta con pendiente indefinida es aquella que es paralela al eje y. Para este tipo de recta, no importa el valor de la y, la x se mantiene constante. Una ecuación para este tipo de recta es x = a. Por ejemplo x = 5
Sea la recta: y = mx + b, una recta paralela a ella tendría como pendiente m.
Recta perpendicular
Una recta perpendicular a otra tendría como pendiente la inversa negativa de la pendiente que es su original.
Sea la recta: y = mx + b una recta perpendicular a ella tendría como pendiente
-(1/m).
Intercepciones:
Las rectas cuando interceptan los ejes x o y, es:
- Intercepta al eje y cuando x = 0
- Intercepta al eje x cuando y = 0
Suponiendo la ecuación y = 2x + 3.
- Intercepta al eje x, si y = 0, entonces:
0 = 2x + 3
2x = -3
x = -3 / 2
x = -1.5
Aplicaciones:
Las ecuaciones lineales se utilizan en una amplia variedad de aplicaciones, como:
- Modelar relaciones entre variables: Por ejemplo, se puede usar una ecuación lineal para modelar la relación entre la temperatura y el número de chirridos que emiten los grillos.
- Resolver problemas: Por ejemplo, se puede usar una ecuación lineal para calcular el costo total de comprar una cierta cantidad de productos.
- Ejercicios de decisión: como el del ejercicio a continuación.
Ejercicio:
La señor Julio Benítez se dedica a la venta de paquetes de cómputo y tiene que elegir entre las siguientes opciones:
- Sueldo base mensual de $4000 más 4% de comisión sobre las ventas realizadas en el mes.
- Sueldo mensual de $2500 más 5% de comisión sobre las ventas realizadas durante el mes.
- Sueldo base mensual de $4500 más 2.6% de comisión sobre las ventas realizadas durante el mes.
- Comisión de 6% sobre las ventas realizadas durante el mes.
Cada paquete de cómputo tiene un valor de $6,000.
Usted, ¿qué le recomendaría a la señora Benítez? ¿Por qué?
Solución.
Solucionarlo con ecuaciones lineales implica crear las ecuaciones. Consideremos a x la cantidad de paquetes de computo vendidos y la variable y los ingresos de del Sr. Benítez tenemos que para las opciones:
- y = (6,000)(0.04)x + 4,000 = 240x + 4,000
- y = (6,000)(0.05)x + 2,500 = 300x+ 2,500
- y = (6,000)(0.026)x + 4,500 = 156x + 4,500
- y = (6,000)(0.06)x = 360x
El que cuenta con la pendiente más pronunciada es la opción 4.
En los puntos donde se interceptan las líneas es donde el Sr. Benítez gana lo mismo. En la gráfica la primera intersección se da entre la opción 3 y la opción 1. Para saber el punto exacto donde ello sucede igualamos las ecuaciones.
240x + 4,000 = 156x + 4,500
240x - 156x = 4,500 - 4,000
84x = 500
x = 500/84 = 5.95 ~ 6
Si la venta es menor a 6 paquetes la mejor opción es la 3. Pero si se venden más la opción 1 es mejor que la 3.
La recta de la opción 1 luego se intercepta con la recta de la opción 2. El punto de intercepción es:
240x + 4,000 = 300x+ 2,500
240x - 300x = 2,500 - 4,000
-60x = -1,500
x = -1,500/-60 = 25
Si las ventas de paquetes están entre 6 y 25 al mes la mejor opción sería la 1, arriba de 25 paquetes la opción 2 es más redituable.
Si seguimos observando la gráfica la opción 4, se vuelva más atractiva cuando las ventas superan los 40 paquetes. Para ser precisos busquemos la intercepción de las rectas de la opción 2 y la 4.
360x = 300x+ 2,500
360x - 300x = 2,500
60x = 2,500/60 = 41.67 ~ 42
Es decir entre 26 y 41 paquetes vendidos la mejor opción es la 2 pero para ventas arriba de 42 paquetes la mejor opción es la 4.
En resumen:
| Rango de ventas | Mejor opción | |
|---|---|---|
| 0 - 5 | Opción 3 | |
| 6 - 25 | Opción 1 | |
| 26 - 41 | Opción 2 | |
| 42 - en adelante | Opción 4 |
Ejercicio (Análisis del punto de equilibrio).
Para un fabricante de relojes, el costo de mano de obra y de los materiales por reloj es de $21 y los costos fijos son de $2500 al día. Si vende cada reloj a $30, ¿cuántos relojes deberá producir y vender cada día con objeto de garantizar que el negocio se mantenga en el punto de equilibrio?

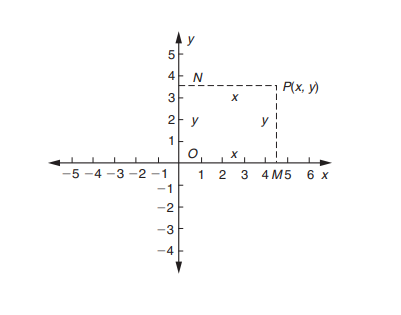









Comentarios
Publicar un comentario