Funciones cuadráticas

 Funciones cuadráticas.



Una función cuadrática es de la forma:

f(x) = ax2 + bx + c


Donde a es diferente a cero.

Las funciones cuadráticas también se les conoce como parábolas.

Cuando a > 0 la parábola abre hacia arriba y cuando a < 0 la parábola abre hacia abajo.

El vértice de una parábola es el punto más bajo cuando a > 0 o el punto más alto cuando a < 0 y se determina con las siguientes fórmulas:



La parábola es simétrica con respecto a la recta vertical que pasa por el vértice. Esta recta se conoce como eje de la parábola. (La línea punteada en la figura)

Ejemplo:

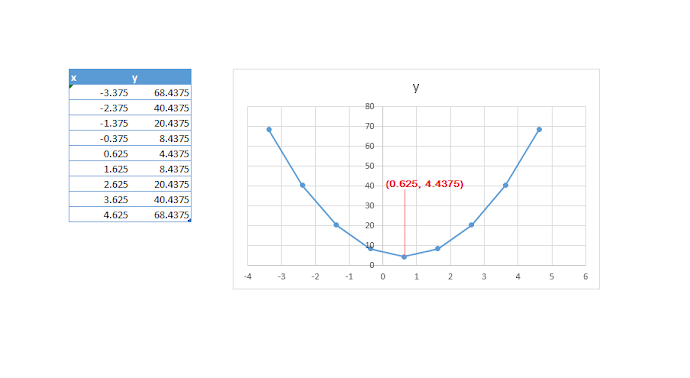
Diagrame y encuentre el vértice de la siguiente función y = 4x2 - 5x + 6.

El vértice:

El vértice es (0.625, 4.4375)

Ejemplo aplicado. Maximizar.

La demanda mensual x de cierto artículo al precio de p dólares por unidad está dada por la relación:

x = 1350 - 45p 

El costo de la mano de obra y del material con que se fabrica este producto es de $5 por unidad y los costos fijos son de $2000 al mes. ¿Qué precio por unidad p deberá fijarse al consumidor con la finalidad de obtener una utilidad máxima mensual?

Solución:

La ecuación de ingresos es precio unitario por cantidad.
La ecuación de costos es costo fijo más costo variable.
La ecuación de utilidad es ingresos menos costos


Ingresos:                  I = px = p(1350 - 45p) = -45p2 + 1350p
Costos:                    C = 5x + 2000 = 5(1350 -45p) + 2000 = 8750 - 225p
Utilidad:                 U = I - C = -45p2 + 1350p - (8750 -225p) = -45p2 + 1575p - 8750

En la ecuación de utilidad a = -45 una parábola que abre hacia abajo, entonces el punto máximo es el vertice.


Comentarios

Publicar un comentario

Entradas más populares de este blog

La línea recta y ecuaciones lineales.

Imagen
Introducción. Una relación entre dos variables por lo regular se expresa mediante de una ecuación algebraica que contiene las dos variables. Por ejemplo, si x es la longitud (en centímetros) del lado de un cuadrado y si y es su área (en centímetros cuadrados), entonces la relación entre x y y se expresa por la ecuación y = x 2 . Para cada valor de x, el valor respectivo de y se obtiene elevando al cuadrado el valor de x.  Las expresiones algebraicas se pueden representar en gráficas, en planos cartesianos. Imagen 1: plano cartesiano En un plano cartesiano, el eje horizontal generalmente se toma como el eje de las x (la variable independiente de las funciones o ecuaciones) y el eje vertical para la variable dependiente y. En el punto donde los ejes se interceptan: x = 0 y y= 0. Puntos en el plano. Un punto en el plano cartesiano se representa con un par de números entre paréntesis; el primer valor representa a x y el segundo a y, por ejemplo:  (-4, 3) (3, 2) (-4, -2) (4, -3) Llamemos a
Leer más

Sistema de Ecuaciones

Imagen
  Sistemas de ecuaciones. Un sistema de ecuaciones es un conjunto de dos o más ecuaciones que se deben resolver al mismo tiempo para encontrar los valores de las incógnitas que satisfacen todas las ecuaciones del sistema. En otras palabras Es un conjunto de relaciones matemáticas que vinculan entre sí a dos o más variables. Las variables se denominan incógnitas y se representan por letras como x, y, z, etc. Las ecuaciones se expresan como igualdades que contienen las incógnitas y valores numéricos conocidos. Ejemplo: Un sistema de ecuaciones con dos incógnitas (x e y) podría ser: x + y = 5 x - y = 1 En este caso, la solución del sistema sería el par de valores (x, y) que hace que ambas ecuaciones sean ciertas al mismo tiempo. En este caso, la solución es x = 3 e y = 2. Tipos de sistemas de ecuaciones Sistemas lineales: Son aquellos en los que las incógnitas solo están elevadas a la primera potencia. Sistemas no lineales: Son aquellos en los que las incógnitas están elevadas a potencias
Leer más