Función potencia

 Función potencia.

Este tipo de funciones es de la forma:

f(x) = axⁿ

en donde a y n son constantes distintas de cero, se denomina función potencia.

Si n = 2, entonces tendremos funciones cuadráticas. La gráfica de y = ax² es una parábola con vértice en el origen, que se abre hacia arriba si a > 0 o hacia abajo si a < 0.

Si n = 1/2. La función f(x) = ax^1/2 es media parábola que abre hacia la derecha. Si a > 0 entonces abrirá por arriba del eje de las x y su a < 0 abrirá por debajo.

Si n = - l: En este caso, f(x) = a/x. El dominio de f(x) consta de todos los números reales excepto cero. Las figuras contiene las gráficas de y = 1/x y y = -1/x (es decir, las correspondientes a a +- 1). La gráfica de y = a/x cuando a > 0 tiene una forma similar a la de y = 1/x y en el caso de que a < 0 es parecida a la forma de y = -1/x. La gráfica de y = a/x se denomina una hipérbola rectangular. A medida que x se acerca a cero, el denominador de f(x) = a/x se hace muy pequeño, de modo que f(x) tiende a ser numéricamente muy grande. Puede llegar a ser grande y positivo o grande y negativo, dependiendo de los signos de a y de x. Estas posibilidades se ven claras en los diagramas. Se dice que el eje de las y es una asíntota vertical de la gráfica.

En la gráfica puede verse que conforme x se vuelve más grande (positivo o negativo), f(x) se acerca cada vez más a cero; sin embargo, jamás es igual a cero. Se dice que el eje x es una asíntota horizontal de la gráfica.

Si n = 3: f(x) = ax³. La gráfica de f(x) es la curva cúbica que aparece en la figura. El dominio es igual al conjunto de todos los números reales.

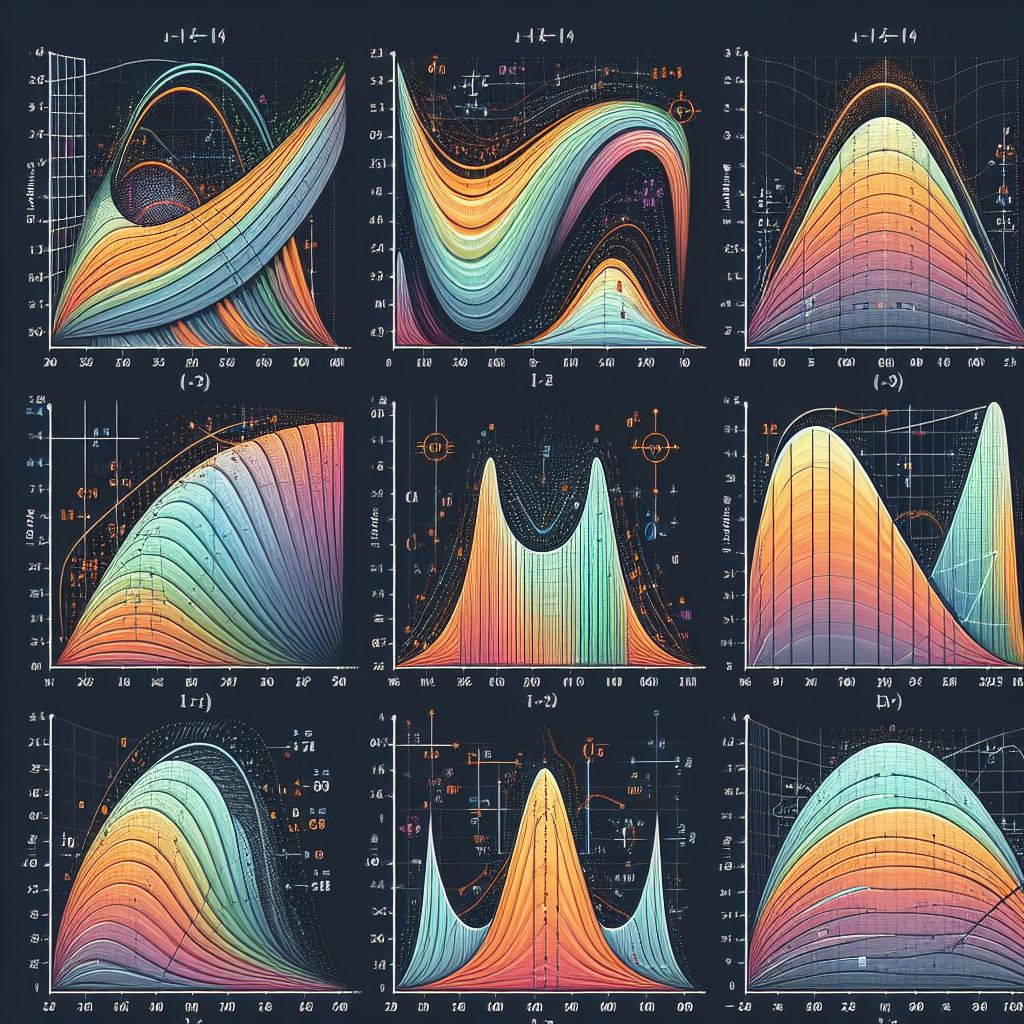
La siguiente figura compara las gráficas de la función y = axⁿ para varios valores de n. Sólo se consideró el caso en que a > 0, y las gráficas se dibujaron, en el cuadrante en que x y y no son negativas. En administración y economía, por lo regular estamos interesados en variables que sólo toman valores no negativos.

Note que todas pasan por el punto (1, a).

Círculos

Un círculo es el conjunto de puntos que están situados a una distancia constante (llamada el radio) de un punto dado (denominado el centro). Determinemos la ecuación del círculo con centro en el punto (h, k) y radio r. Sea (x, y) cualquier punto sobre el círculo. La distancia entre este punto (x, y) y el centro (h, k) está dada por la fórmula de la distancia que es 

Es decir, el radio r es:

Si elevamos al cuadrado, obtenemos la forma centro-radio de la ecuación de un círculo.

Si el centro es el origen (0,0), es decir, h = k = 0 y la ecuación (1) se reduce a:

En la práctica, sólo la porción de la curva situada en el primer cuadrante tiene sentido práctico.

Ejercicio 1.

Determine la ecuación del círculo con centro en (2, -3) y radio 5.

Ejercicio 2.

Determine si la siguiente expresión es un circulo. Si es así, encuentre su centro y su radio.

Ejercicio 3. (Curva de transformación de productos) 

Una empresa que fabrica zapatos puede producir zapatos para caballero o para dama modificando el proceso de producción. Las cantidades posibles x y y (en cientos de pares) están relacionadas por la ecuación:

 ¿Cuáles son los números máximos de zapatos de cada tipo que pueden producirse?